导入数据
setwd("~/sites/rblog/content/post/")
df <- read.csv("../../static/data/sh000001.csv")这条代码的意思是:读入(read)一个 csv 文档(csv),文档的名称是“ 000001.csv”,保留表头(header = T),读入后,赋值给数据框变量:df
浏览下数据属性:
str(df)## 'data.frame': 4249 obs. of 9 variables:
## $ date : Factor w/ 4249 levels "2000/1/10","2000/1/11",..: 16 17 18 19 1 2 3 4 5 6 ...
## $ close : num 1406 1410 1464 1517 1545 ...
## $ highest : num 1408 1434 1464 1523 1547 ...
## $ lowest : num 1361 1398 1400 1477 1506 ...
## $ open : num 1369 1408 1406 1477 1532 ...
## $ amount : num 39.79 3.31 54.26 52.66 28.51 ...
## $ rate : num 2.912 0.235 3.849 3.597 1.88 ...
## $ volume : int 9032824 10579392 13480517 34869396 31253046 21924568 15221934 8611943 7447013 7647977 ...
## $ turnover: num 5.80e+09 8.65e+09 1.02e+10 2.21e+10 2.09e+10 ...仔细看下结果,rdata$date 的变量类型是 factor,也就是因子属性,我们需要的是日期属性,将它变为日期类型。
df$date <- as.Date(df$date)计算收益率
金融数据分析一般研究的是资产收益率,而不是资产的价格。资产收益率序列比一般的价格序列更容易处理,更具有研究意义。而资产收益率也有很多种定义,这里使用对数收益率,也就是对上海证券综合指数日收盘价格取对数差分。
close <- df[,2] # 上证指数日收盘价
len <- length(close) # 获取数据的长度
return <- log(close[2:len])-log(close[1:len-1]) # 上证指数的对数收益率这行代码的意思是计算指数的“对数收益率” [2:n]的意思是从第 2 行开始到最后一行,[1:n-1]就是从第 1 行到第 n-1 行,根据的是对数收益率的计算方法。
head(return) #查看 return 的前 6 行数据## [1] 0.002351519 0.037768650 0.035340827 0.018622775 -0.043202296
## [6] -0.028626936股票指数的可视化
在绘制图形之前,我们需要先将数据转化为时间序列格式,需要用到 ts 函数。 用法:ts(数据向量,start=c(第一个数据所表示的年,月),frequency=表示将时间分开的时间间隔)。
Close.ts<-ts(close,start=c(2000),freq=250)
Return.ts<-ts(return,start=c(2000),freq=250)
par(mfrow=c(2,1)) #建立一个以两行一列排列图形的图形窗口
plot(Close.ts,type="l",main="(a) Daily Closing Price of 000001.SH",xlab="Date", ylab="Price", cex.main=0.95,las=1)
plot(Return.ts,type="l",main="(b) Daily Rate of Return of 000001.SH",xlab="Date", ylab="Rate", cex.main=0.95, las=1)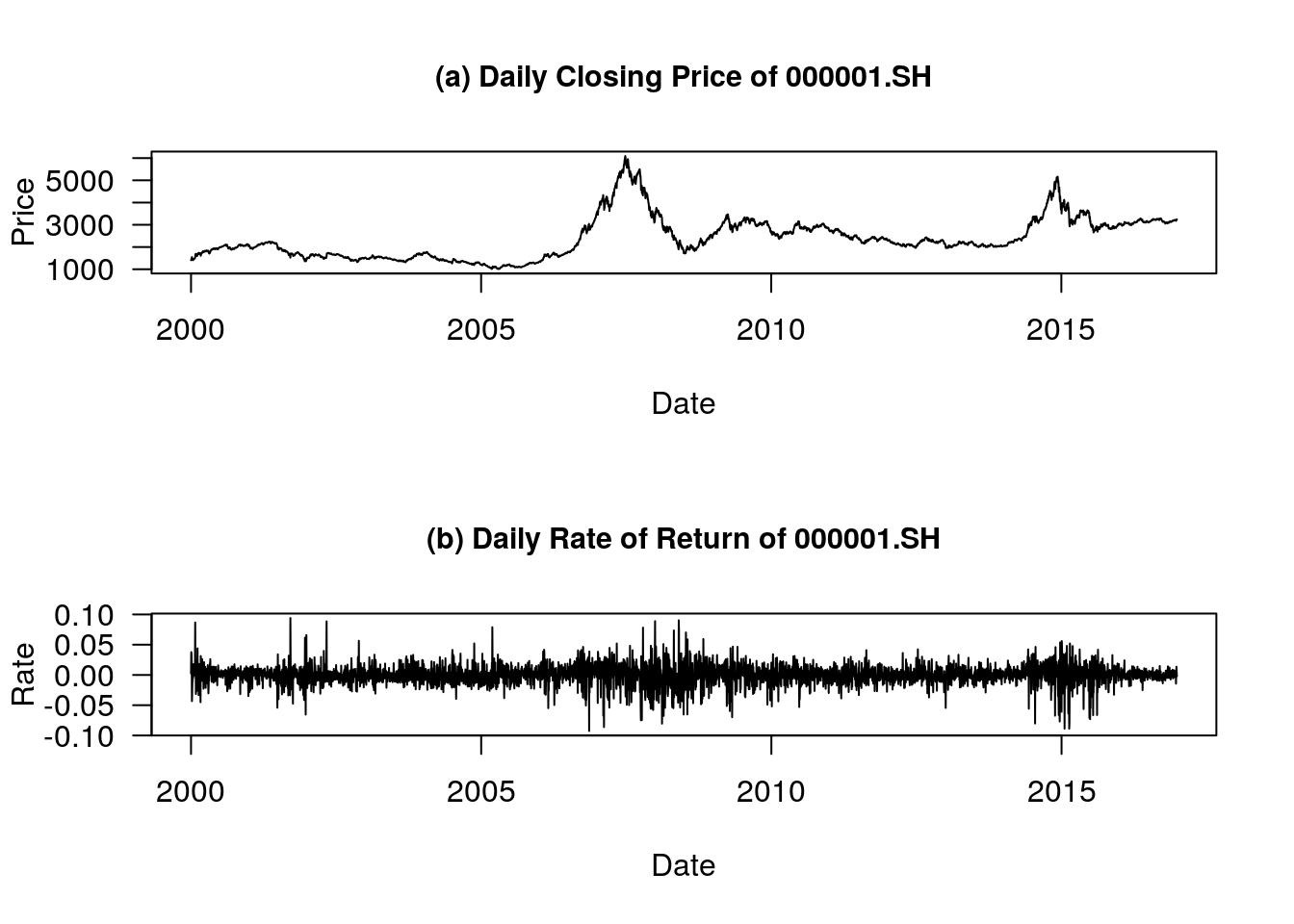
上面的代码中,type、main、xlab、ylab、cex.main、las 都是图形参数。 其中位于下方的图就是上海证券综合指数的日收盘价(上)和日收益率(下)的时序图。 从图形分析结果来看,2008 年和 2015 年两个时间段有明显的波动聚集现象。
股票收益率的基本统计量
在做模型拟合之前需要对数据做一个基本的了解,先求解数据的一些基本统计量。
library(tseries)## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoou<-sum(return)/len # 求均值
e<-sqrt(sum((return-u)^2)/(len-1)) # 求标准差
s<-sum((return-u)^3)/((len-1)*e^3) # 求偏度
k<-sum((return-u)^4)/((len-1)*e^4) # 求峰度
jarque.bera.test(return) # JB 正态性检验##
## Jarque Bera Test
##
## data: return
## X-squared = 3958.7, df = 2, p-value < 2.2e-16由结果我们可以得出上海证券综合指数的对数收益率的均值为 0.000196,标准差为 0.016129,偏度系数为 -0.246041,峰度系数为 7.678296,以及从正态性检验结果的 P 值接近于 0,也就是说上证指数日对数收益率不是正态分布,呈现左偏分布,且有高峰厚尾的现象。
ACF 图和 PACF 图
使用自相关函数(ACF)和偏自相关函数(PACF)来对收益率序列的自相关性进行分析。
par(mfrow=c(2,1))
acf(return,main='',xlab='Lag (a)',ylab='ACF',las=1) #画自相关图
title(main='(a) the ACF of Return',cex.main=0.95) #为图形加标题,并设置标题大小
pacf(return,main='',xlab='Lag (b)',ylab='PACF',las=1) #画偏自相关图
title(main='(b) the PACF of Return',cex.main=0.95)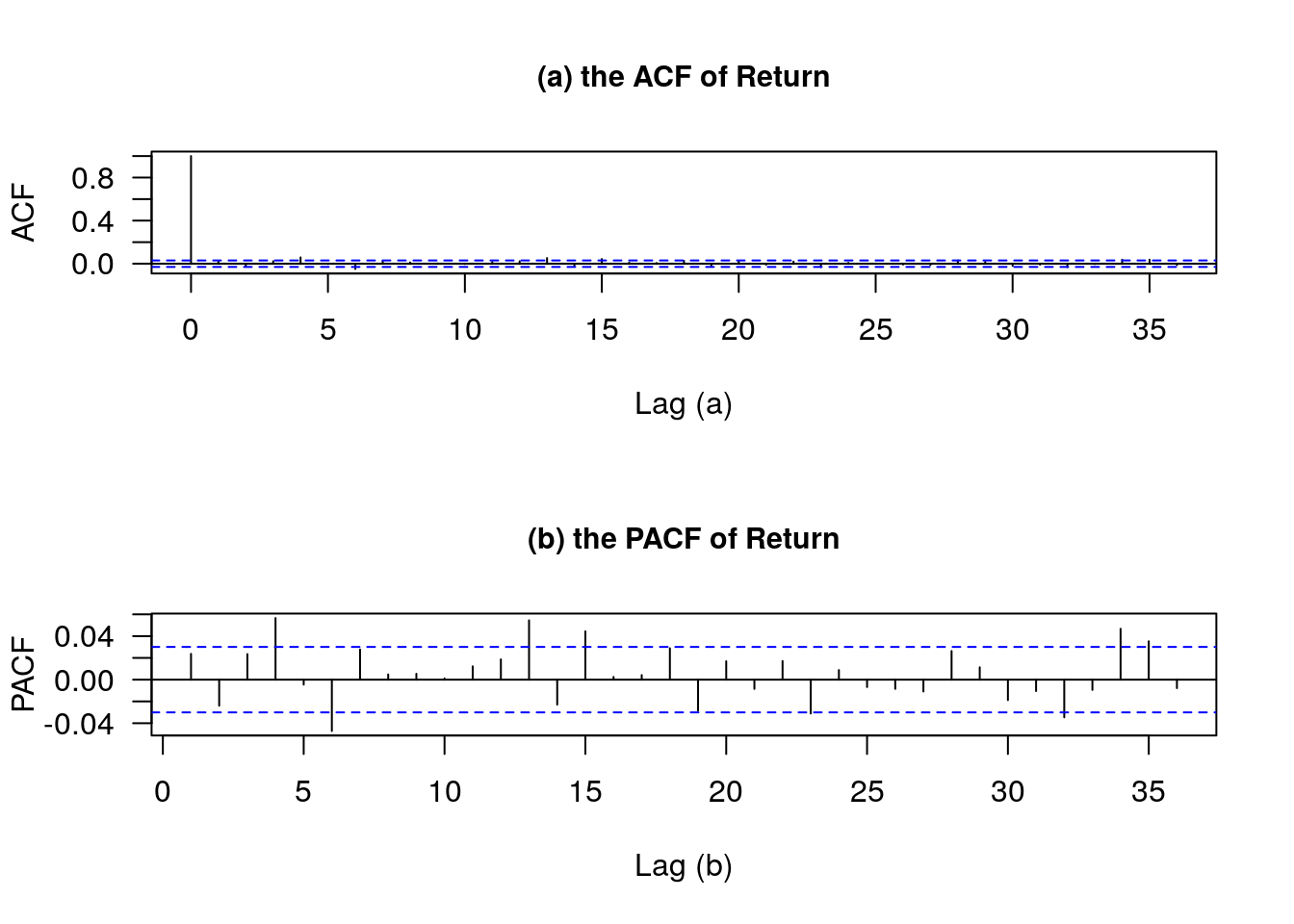
由收益率序列(return)的 ACF 图和 PACF 图可以得出:两个图大部分函数值在置信区间内(图中蓝色虚线区域)上下跳跃,所以收益率序列自相关性很低,或者说具有很弱的自相关性,因此在条件期望模型中不需要引入自相关性部分,满足 GARCH 模型中的均值方程,收益率由一个常数项加上一个随机扰动项组成。
虽然收益率序列基本不具有自相关性,但是要拟合 GARCH 模型,我们还需要考察收益率平方的自相关性。
par(mfrow=c(2,1))
return.square<-return^2
acf(return.square,main='',xlab='Lag (c)',ylab='ACF',las=1)
title(main='(a) the ACF of Return Square',cex.main=0.95)
pacf(return.square,main='',xlab='Lag (d)',ylab='PACF',las=1)
title(main='(b) the PACF of Return Square',cex.main=0.95)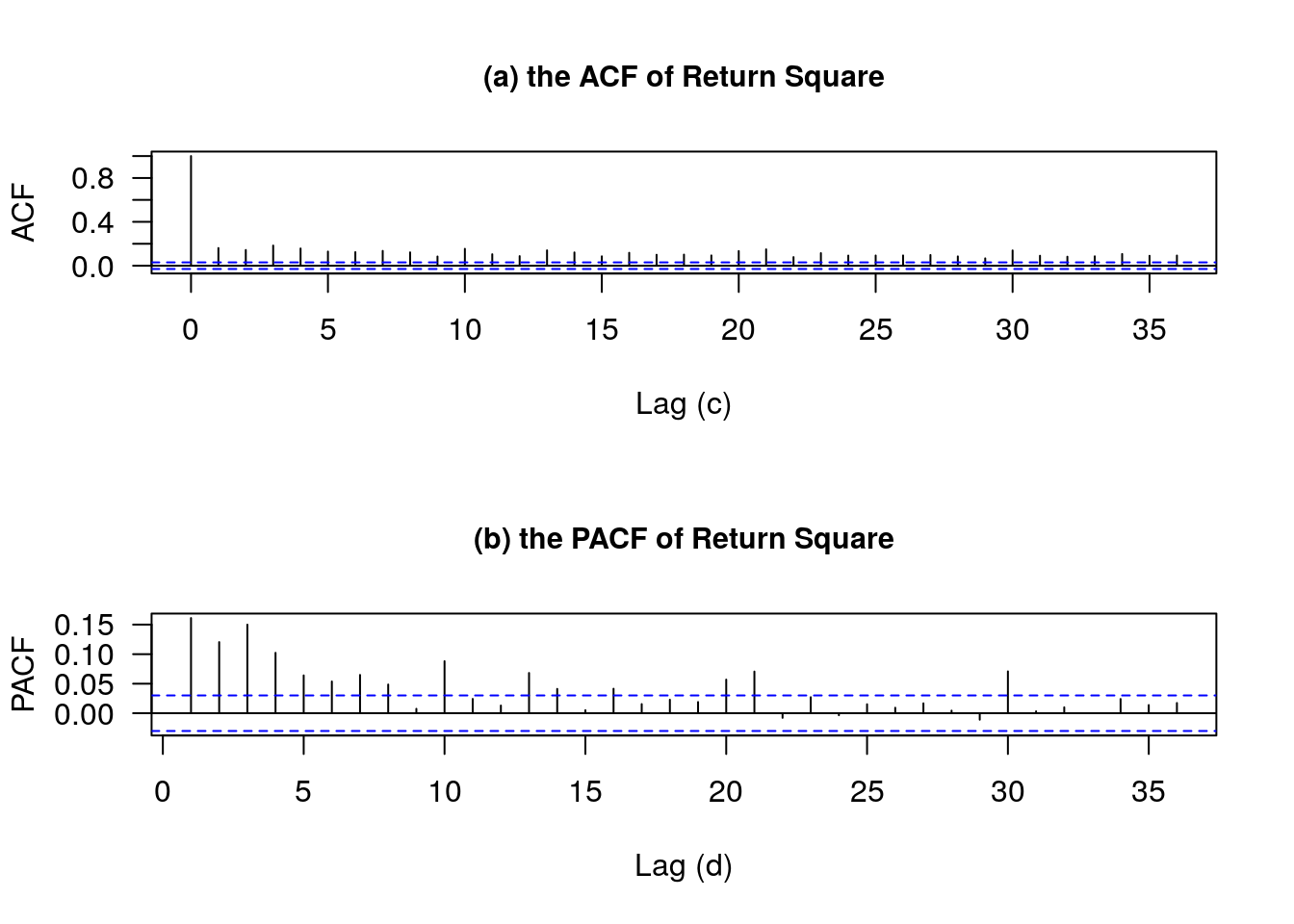
尽管股价收益率序列的 ACF 值揭示了其弱相关性,但收益率平方的 ACF 值 却表现出了一定的相关性和持续性,其大部分值都超过了置信区间(图中蓝色虚线)。注意到收益率平方的 ACF 值在滞后 3、10、21、30 期后都有缓慢衰退,说明了方差序列具有一定程度的序列相关性,因此采用 GARCH 模型来描述股价波动过程中的条件方差。
ARCH 效应的检验
收益率的时序图表明,在日收益率数据中可能存在 ARCH 效应,如果存在 ARCH 效应,则可以进行 GARCH 模型的拟合。反之,不能用 GARCH 模型拟合方程。
ARCH 效应的检验,可以用 FinTS 包中的 LM 检验,具体用法如下:
library(zoo)##
## Attaching package: 'zoo'## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numericlibrary(FinTS) #LM 检验
ArchTest(return,lag=12) #滞后 12 期##
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: return
## Chi-squared = 389.3, df = 12, p-value < 2.2e-16检验的原假设是:不存在 ARCH 效应。检验结果为卡方统计量的值为 389.3,对应的 P 值几乎为 0,也就是说在 1% 的显著性水平上拒绝原假设,从而拒绝不存在 ARCH 效应的假设,收益率序列存在 ARCH 效应,可以进行 GARCH 模型的拟合。 存在 ARCH 效应的意思是,以往的波动率的高低,会对今天的收益的波动率的高低产生影响。